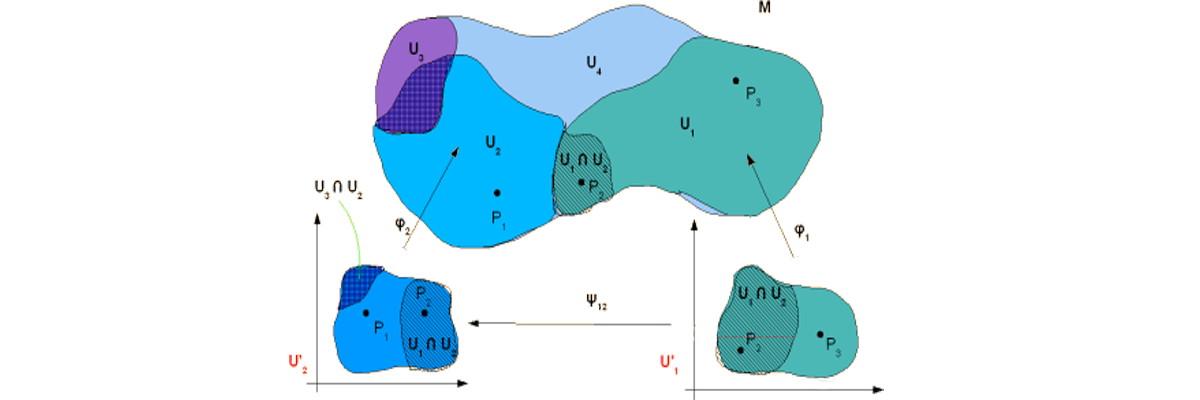
Computational differential geometry describes calculus on a manifold.

John Ernsthausen identified and implemented examples for the numerical differential-algebraic equation (DAE) integration methods developed in Rheinbold’s package DAEPAK. As Werner C. Rheinbold’s and Patrick J. Rabier’s graduate student, John assisted in the documentation and debugging of the FORTRAN77 subroutines in DAEPAK. The experience required a deep understanding of the numerical differential geometry package MANPAK, a collection of numerical algorithms implementing computational differential geometry for submanifolds of $R^n$.

Computational differential geometry

A subset $M$ of $R^n$ is a manifold whenever a chart exists near each point in $M$, roughly speaking. For example, a road map near your current location on Earth is a chart from flat $R^2$ into the surface of Earth, a 2-dimensional submanifold of $R^3$.

More precisely, whenever each point in a subset of $R^d$ can be diffeomorphically mapped into a (non-empty) subset of $M$ in $R^n$, with $d \leq n$, and the smoothness of the diffeomorphism is $k \geq 1$, then $M$ is a $d$-dimensional $C^k$ submanifold of $R^n$. The diffeomorphism is a local parameterization, and the inverse of a local parameterization is a chart.

Differential geometry enables calculus on a (nonempty) submanifold $M$ of $R^n$. Given any point $x_c \in M$, there is a local parameterization near $x_c \in M$. All local parameterizations near $x_c \in M$ are an equivalent class, and the particular local parameterization is a representative from it. Locally near $x_c$, a DAE can be reduced to an ordinary differential equations on a manifold. In this point of view, the path constructed by projecting any solution to the DAE through the local parameterization is a solution to the equivalent ordinary differential equation on a manifold, and the unique solution of that local ordinary differential equation on a manifold lifted through the representative local parameterization must be the unique solution of the DAE.

Ordinary differential equations describe dynamics in $R^n$. Ordinary differential equations on a manifold describe dynamics restricted to the manifold. The solutions to ordinary differential equations on a manifold must live in the manifold.

Differential geometry is discussed in the language of submersions, immersions, and diffeomorphisms for the purpose of constructing a coordinate subspace, local parameterization, and tangent space near each point in the submanifold embedded into the ambient space $R^n$. These concepts are discussed in the MANPAK article [R1996] and the Rabier and Rheinboldt book [RR2002].

While all these topics are required to understand the mathematics behind computational differential geometry, a deep understanding of these topics is not required to apply the results. Local parameterizations and their derivatives for general submanifolds of $R^n$ are constructed in the software package MANPAK. DAEPAK is built on the software package MANPAK.

LITERATURE

R1996

Rheinboldt W.C.: MANPAK: A set of algorithms for computations on implicitly defined manifolds. Computers & Mathematics with Applications, 32(12), 15-28 (1996). [link].

RR2002

Rabier P.J. and Rheinboldt W.C.: Theoretical and numerical analysis of differential-algebraic equations. In: P.G. Ciarlet, J.L. Lions (eds.) Solution of Equations in $R^n$ (Part 4), Techniques of Scientific Computing (Part 4), Handbook of Numerical Analysis, vol 8, pp. 183-540. Elsevier, Amsterdam (2002) [link].